insertion sort algorithm python

Overview

In this article I am going to walk through an array sorting algorithm called "Insertion sort" in short and clear steps; hopefully to help you understand more how sorting algorithms work in Python in order to enhance your abilities to analyze and solve problems more efficiently.

Before we start

Before we start, you have to know that in order to achieve the best sorting method, and to be able to compare all methods and algorithms together in respect of time and space; Big O is the perfect measure for that.

Big O Notation is a mathematical concept used to describe the complexity of an algorithm as how much time and memory it holds.

Assuming that n is the size of the input to an algorithm, the Big O notation represents the relationship between n and the number of steps the algorithm takes to find a solution.

The following description of some cases will help you understand and classify Big O notation accordingly:

Big O	Complexity	Description
O(1)	Constant	fixed time/space in each time an algorithm is executed.
O(n)	Linear	linearly growth with data size until it reaches O (worst case)
O(n²)	quadratic	directly proportional to square data size "common in nested iterations"
O(2^n)	exponential	double growth with addition of data ex: recursive Fibonacci
O(log n)	logarithmic	little effect on growth while doubling data size

Insertion Sort

The insertion sort algorithm takes each element of the array and compares it to the rest of elements and then puts each element in its right place.

The next Pseudocode shows how to implement the insertion sort algorithm:

 InsertionSort(int[] arr)

    FOR i = 1 to arr.length

      int j <-- i - 1
      int temp <-- arr[i]

      WHILE j >= 0 AND temp < arr[j]
        arr[j + 1] <-- arr[j]
        j <-- j - 1

      arr[j + 1] <-- temp

Lets assume the input of our algorithm is the following array/list:

array = [8, 4, 23, 42, 16, 15]

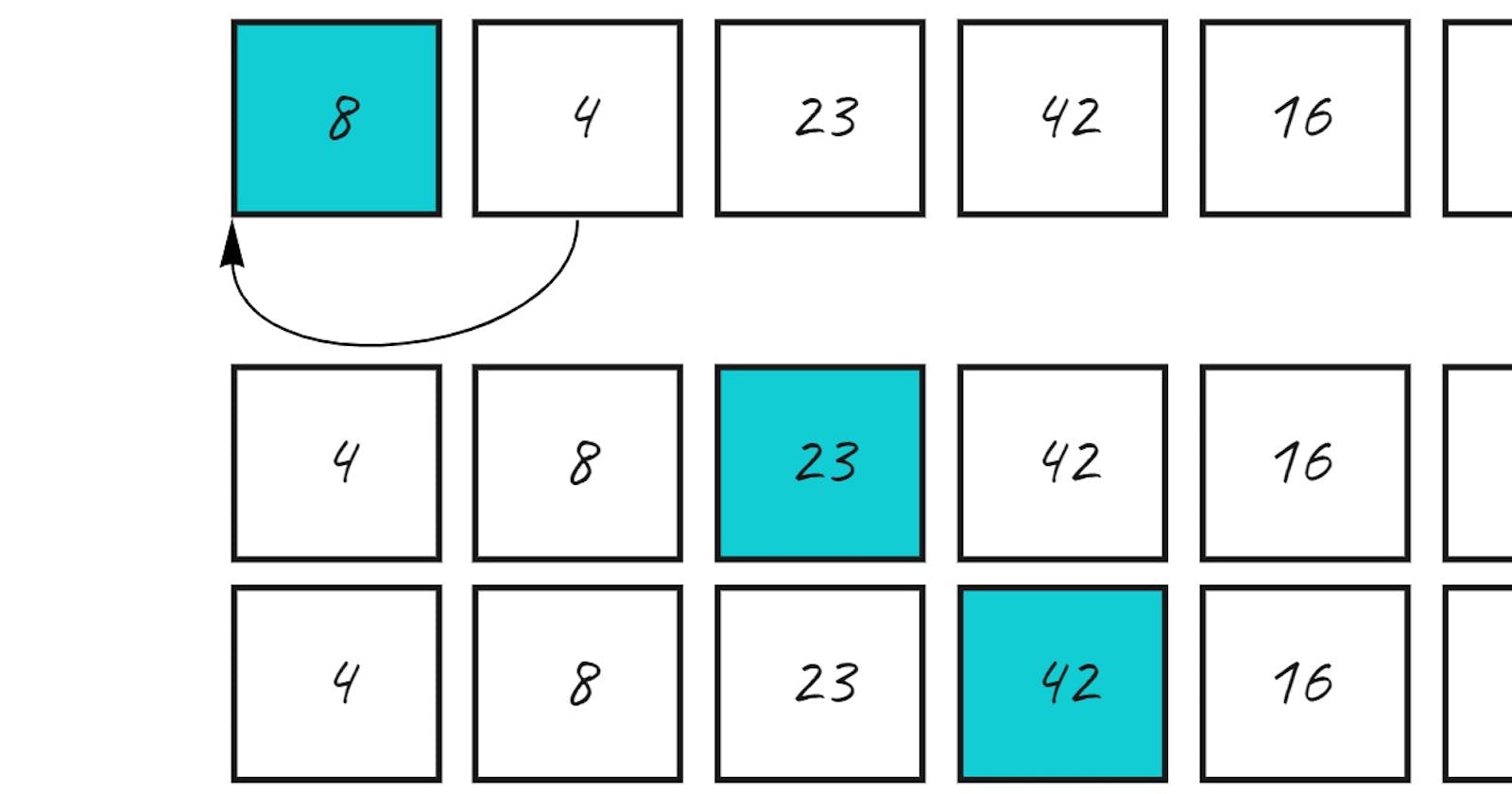
To make it more clear and easy to understand, here is a step-by-step visualization of each algorithm iteration for the array:

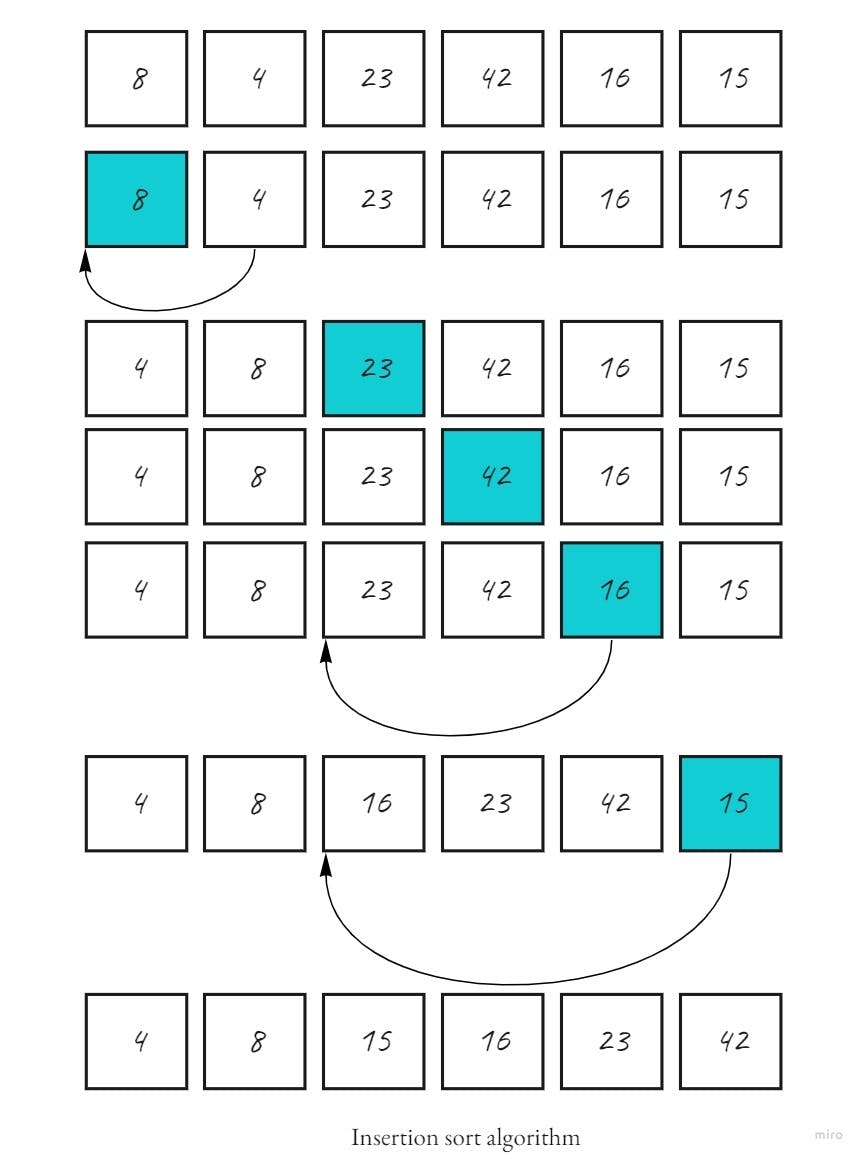
As you can see, the array is supposed to be sorted ascendingly by taking each element at a time and compare it to the rest of elements values, and when it finds a smaller value, it changes its position to be inserted before that value.

Algorithm

Now, lets review the steps of solving this problem so we can implement it using Python:

Define a function that takes an array of integers as an argument.
Iterate through the array with (i) as index, starting from the second element in the array up to the last.
Create a variable temp to track the element I want to look for its correct position.
Create a variable j to equal the elements before temp.
Use while to loop through the list and compare temp to j values.
Start shifting elements to place temp element according to the values, to be sorted ascendingly.
Return the sorted array.

Code Implementation

Here is the implementation of Python code for Insertion sort approach, built upon the algorithm steps above:

def insertion_sort(array):

    for i in range(1, len(array)):
        j = i - 1  
        temp = array[i]   

        while j >= 0 and temp < array[j]:
            array[j+1] = array[j]
            j -= 1

        arr[j + 1] = temp
    return array

Assuming array = [8, 4, 23, 42, 16, 15].
By stepping through the code and after creating j: where it stores all values before temp, and temp: which tracks the element we want to find the position for, we started to compare each element starting from the second element: temp = 4.
We checked if j is larger than 0, which is correct j = 8, and if 4 is less that 8 -which is True- we will shift j value to be in the next position --> [8, 8, 23, 42, 16, 15].
Then we will add the temp in its right place --> [4, 8, 23, 42, 16, 15].
Now we move to the next temp value that achieves the while conditions, which is 16, while j will be [4, 8, 23, 42] and 16 is less than 23 so 23 is going to be shifted and 16 is going to take its place --> [4, 8, 16, 23, 42, 15]
The third shift happens when temp = 15 and j = [4, 8, 16, 23, 42], here 15 is less than 16 to 16 is going to be shifted to the right and 15 will take its place to leave the array looking like this --> [4, 8, 15, 16, 23, 42]
After achieving this result we return the new sorted array.

Big O Notation

You can clearly notice that the code has two nested loops: For loop and While loop, each loop has a time complexity O(n).

The best case scenario happens if we had an already sorted array, that will prevent the inner loop form execution and then the runtime complexity will be O(n).

The worst case scenario is happens if we had a descending ordered array which will make n executions of the inner loop, and that will give us a runtime complexity of O(n²).

And that makes the Big O time complexity of insertion sort function is O(n²)

User Acceptance Tests

Here is a passed test of insertion_sort function with different arrays:

def test_insertion_sort():
    array = [8,4,23,42,16,15]
    assert [4, 8, 15, 16, 23, 42] == insertion_sort(array)

    array2 = [5,12,7,5,5,7]
    assert [5, 5, 5, 7, 7, 12] == insertion_sort(array2)

    array3 = [20,18,12,8,5,-2]
    assert [-2, 5, 8, 12, 18, 20] == insertion_sort(array3)

Source Code

GitHub

Insertion Sort Algorithm

Step-by-Step with Python

Table of contents